2次関数のグラフ高校数学

たむかい学習教室
8月22日
読了時間: 7分

2次関数のグラフ高校数学

当ブログでは、授業のポイント解説をしています。

学校の夏休みも後半に入っています。塾生は１学期の復習や受験対策を行っています。高校数Ⅰでは、2次関数の単元に入り、平方完成やグラフの軸と頂点など、式のつくり方やグラフの表し方について復習を進めています。

放物線の平行移動

問題

次の関数のグラフをｘ軸方向に－１、ｙ軸方向に１だけ平行移動したグラフの方程式を求めよ。

1）ｙ＝２ｘ²

2）ｙ＝ｘ²－２ｘ＋３

1）

ｙ＝２ｘ²

グラフの頂点は（０，０）

移動後の頂点は（－１，１）

よって、

ｙ＝２（ｘ＋１）²＋１

2）

ｙ＝ｘ²－２ｘ＋３より

ｙ＝（ｘ－１）²－１＋３

ｙ＝（ｘ－１）²＋２

頂点は（１，２）

移動後の頂点は（０，３）

よって、求める方程式は、

ｙ＝ｘ²＋３

問題

ｙ＝－３ｘ²＋２ｘ＋１のグラフは、ｙ＝－３ｘ²－２ｘ－１のグラフをどのように平行移動すれば得られるか。

ｙ＝－３ｘ²＋２ｘ＋１より

ｙ

＝－３（ｘ²－2/3ｘ）＋１

＝－３｛（ｘ－1/3）²－1/9｝＋１

＝－３（ｘ－1/3）²＋4/3

頂点は（1/3，4/3）

ｙ＝－３ｘ²－２ｘ－１より

ｙ

＝－３（ｘ²＋2/3ｘ）－１

＝－３｛（ｘ＋1/3）²－1/9｝－１

＝－３（ｘ＋1/3）²－2/3

頂点は（－1/3，－2/3）

２点のｘ座標より

1/3－（－1/3）

＝2/3

２点のｙ座標より

4/3－（－2/3）

＝２

よって、

ｘ軸方向に2/3、ｙ軸方向に２

問題

次の条件をみたす2次関数のグラフの方程式を求めよ。

1）頂点が（２，１）で、点（３，－１）を通る

2）ｘ軸と２点（１，０）、（３，０）で交わり、ｙ切片が３

1）

頂点（２，１）より

ｙ＝ａ（ｘ－２）²＋１

点（３，－１）を通るから

ａ（３－２）²＋１＝－１

ａ＝－２

よって、

ｙ＝－２（ｘ－２）²＋１

2）

ｘ切片が１と３だから

ｙ＝ａ（ｘ－１）（ｘ－３）

ｙ切片が３で、

（０，３）を通るから

ａ・（－１）・（－３）＝３

ａ＝１

よって、

ｙ＝（ｘ－１）（ｘ－３）

3）３点（－１，－２）、（１，６）、（２，７）を通る

4）３点（－１，２）、（１，２）、（２，５）を通る

3）

求める２次関数を

ｙ＝ａｘ²＋ｂｘ＋ｃとする

それぞれのｘとｙの値を代入

ａ－ｂ＋ｃ＝－２　　①

ａ＋ｂ＋ｃ＝６　　　②

４ａ＋２ｂ＋ｃ＝７　③

①－②

　　ａ－ｂ＋ｃ＝－２

－）ａ＋ｂ＋ｃ＝６

　　　　　　ｂ＝４

②－③

　　　ａ＋　ｂ＋ｃ＝６

－）４ａ＋２ｂ＋ｃ＝７

　－３ａ－　ｂ　　＝－１

３ａ＋ｂ＝１

ｂ＝４を代入

３ａ＋４＝１

ａ＝－１

①にａ＝－１、ｂ＝４を代入

－１－４＋ｃ＝－２

ｃ＝３

よって、求める式は、

ｙ＝－ｘ²＋４ｘ＋３

4）

３点（－１，２）、（１，２）、（２，５）

ａ－ｂ＋ｃ＝２　　　①

ａ＋ｂ＋ｃ＝２　　　②

４ａ＋２ｂ＋ｃ＝５　③

①－②

　　ａ－ｂ＋ｃ＝２

－）ａ＋ｂ＋ｃ＝２

　　　　　　ｂ＝０

②－③

　　　ａ＋　ｂ＋ｃ＝２

－）４ａ＋２ｂ＋ｃ＝５

　－３ａ－　ｂ　　＝－３

３ａ＋ｂ＝３

ｂ＝０を代入

ａ＝１

②にａ＝１、ｂ＝０を代入

ｃ＝１

よって、求める式は、

ｙ＝ｘ²＋１

5）ｘ軸に接し、２点（０，２）、（２，２）を通る

ｘ軸に接するから、

頂点は、ｙ＝０

（０，２）と（２，２）を通るから、

軸は、ｘ＝１

ｙ＝ａ（ｘ－１）²

（０，２）を代入

ａ（０－１）²＝２

ａ＝２

よって、求める式は、

ｙ＝２（ｘ－１）²

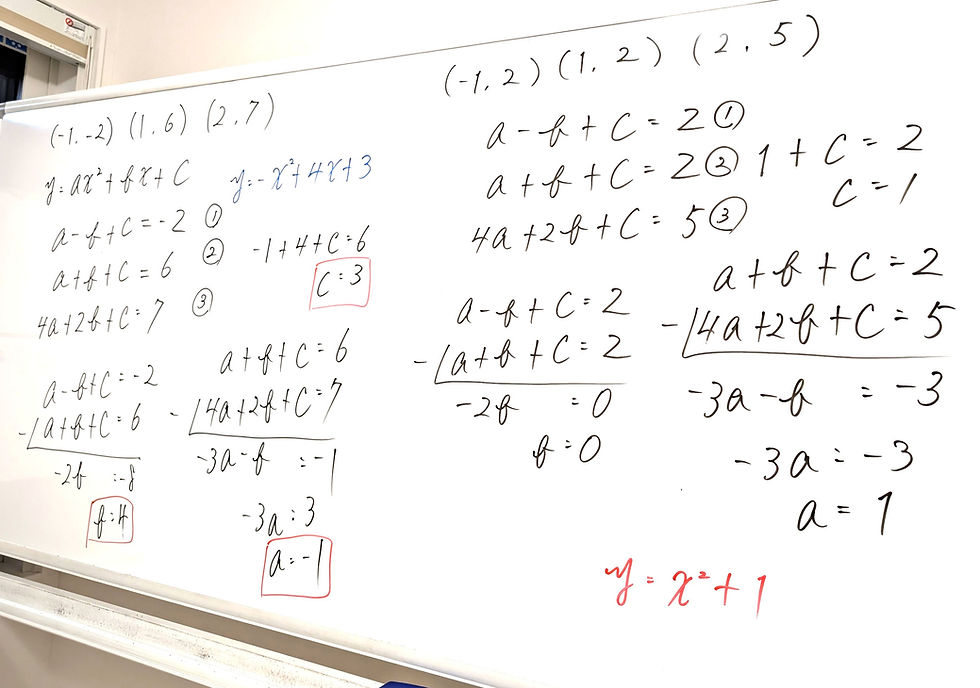
問題

ａ、ｂを定数とする。

放物線

Ｇ：ｙ＝ｘ²＋ａｘ＋ｂ

は、２点（０，２）、（１，１）を通る。

1）

ａ、ｂの値をそれぞれ求めよ。また、Ｇの頂点の座標を求めよ。

2）-ⅰ)

Ｇをｙ軸に関して対称移動した放物線をＣ₁とする。Ｃ₁の方程式を求めよ。

2）-ⅱ)

Ｇをｘ軸に関して対称移動した放物線をＣ₂とする。Ｃ₂の方程式を求めよ。

3）

３つの放物線Ｇ、Ｃ₁、Ｃ₂の頂点をそれぞれＡ、Ｂ、Ｃとし、Ｇを平行移動した放物線のうち、頂点が線分ＢＣ上（両端を除く）にある放物線をＨとする。

さらに、Ｈは点（－1/3，1/3）を通り、線分ＡＣ（両端を除く）と点Ｐで交わり、線分ＡＢ（両端を除く）と点Ｑで交わる。このとき、Ｐ、Ｑの座標をそれぞれ求めよ。

1）

ｙ＝ｘ²＋ａｘ＋ｂに、

（０，２）、（１，１）を代入

ｂ＝２

１＋ａ＋ｂ＝１

ａ＋ｂ＝０

ｂ＝２だから

ａ＝－２

以上から、Ｇの式は、

ｙ＝ｘ²－２ｘ＋２

ｙ＝（ｘ－１）²＋１

よって、求める頂点は、

（１，１）

2）-ⅰ)

ｙ軸に関して対称移動するから、

ｘ座標は異符号になる

ｙ＝ｘ²－２ｘ＋２より

ｙ＝（－ｘ）²－２（－ｘ）＋２

よって、求める式Ｃ₁は、

ｙ＝ｘ²＋２ｘ＋２

2）-ⅱ)

ｘ軸に関して対称移動するから、

ｙ座標は異符号になる

ｙ＝ｘ²－２ｘ＋２より

－ｙ＝ｘ²－２ｘ＋２

ｙ＝－ｘ²＋２ｘ－２

3）

放物線Ｃ₁の頂点

ｙ＝ｘ²＋２ｘ＋２

ｙ＝（ｘ＋１）²＋１

よって、

点Ｂ（－１，１）

放物線Ｃ₂の頂点

ｙ＝－ｘ²＋２ｘ－２

ｙ

＝－（ｘ²－２ｘ）－２

＝－｛（ｘ－１）²－１｝－２

＝－（ｘ－１）²－１

よって、

点Ｃ（１，－１）

線分ＢＣの式は、

Ｂ（－１，１）と

Ｃ（１，－１）を通るから

ｙ＝－ｘ

※２点は両座標どうしがともに異符号

👉原点について対称な点

放物線Ｈの頂点のｘ座標をｔとする

頂点はｙ＝－ｘ上にあるから、

（ｔ，－ｔ）

これにより、Ｈの式を、

ｙ＝（ｘ－ｔ）²－ｔとおく

ただし、

点Ｂ、点Ｃを除くとあるから、

－１＜ｔ＜１　①

点（－1/3，1/3）を通るから、

（－1/3－ｔ）²－ｔ＝1/3

ｔ²－1/3ｔ－2/9＝０

９ｔ²－３ｔ－２＝０

（３ｔ－２）（３ｔ＋１）＝０

ｔ＝2/3、－1/3

どちらの解も①を満たす

ｔ＝2/3のとき

Ｈの式は、

ｙ＝（ｘ－2/3）²－2/3

線分ＡＣは、

（１，１）と（１，－１）を通るから

ｘ＝１の直線

これと交わる点Ｐのｙ座標は、

ｙ＝（１－2/3）²－2/3

　＝1/9－6/9

　＝－5/9

よって、点Ｐの座標は、

（１，－5/9）

線分ＡＢは、

（１，１）と（－１，１）を通るから

ｙ＝１の直線

これと交わる点Ｑのｘ座標は、

（ｘ－2/3）²－2/3＝１

（ｘ－2/3）²＝5/3

ｘ－2/3＝±√5/√3

　　２±√15

ｘ＝━━━━

　　　３

点Ｑは、ｘ＜０だから、

　　２－√15

ｘ＝━━━━

　　　３

よって、点Ｑのｙ座標は、

　２－√15

（━━━━，１）

　　３

ｔ＝－1/3のとき、

Ｈの式は、

ｙ＝（ｘ＋1/3）²＋1/3

線分ＡＣ（ｘ＝１）との交点は、

ｙ＝（１＋1/3）²＋1/3

　＝19/9

ｙ＝19/9となり、交点をもたない。

以上から

点Ｐ（１，－5/9）

　　　２－√15

点Ｑ（━━━━，１）

　　　　３

体験学習受付中！

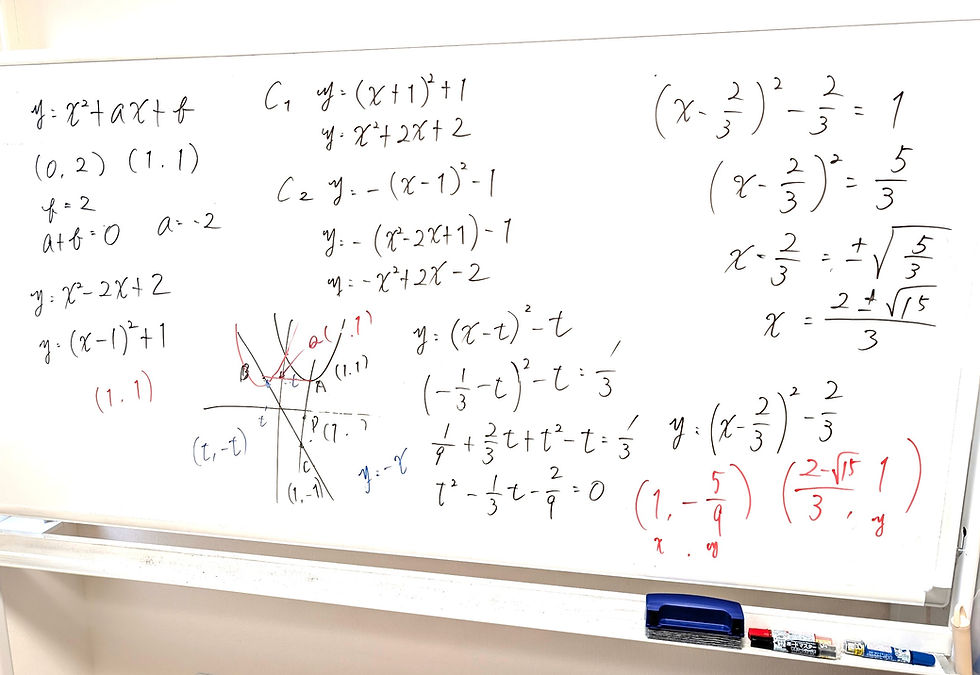
【たむかい学習教室】

完全1対1 個別指導

教員経験２０年のプロ講師による完全マンツーマン指導！

追加料金なしの安心の授業料で、手厚いサポート！

全科目対応で、幅広い学習ニーズにお応えいたします！

塾生のホンネ

「数学や英語が苦手。何から始めたらいい？」

「長い問題文が苦手。どうしたらいい？」

「学校の授業で難しいことが増えてきた」

「受験が不安。テスト成績を上げていきたい」

完全１対１授業でホンネを解決！

★苦手の克服に最適★

★受験に強い個別指導★

★経験豊富な講師の一貫指導★

★安心の授業料で全力サポート★

★苦手の克服に最適★

　５教科対応、完全マンツーマンで指導いたします。弱点を着実に克服でき、「わかる・できる」につながります。学校の授業が定着しやくすなり、成績アップも期待できます。

★受験に強い個別指導★

　入試の出題範囲は広く、十分な対策時間と学習量が必要になります。受験に向けて、対策時間と学習量をしっかりと確保できるのは、完全１対１授業の強みです。

★経験豊富な講師の一貫指導★

　教員経験20年の講師が確かなノウハウで、難解な内容もわかりやすく丁寧に指導いたします。初めての受講生からも「分かりやすい」「納得の解説」と好評です。

★安心の授業料で全力サポート★

　入塾費や高額な教材費、授業料以外にいただく追加料金は一切ございません。安心の授業料で全力サポートいたします。

　＜１か月授業料（税込）＞

　90分授業：14,800円（月4回）

120分授業：17,600円（月4回）

　(例)１回・90分授業の場合

　教師１名・生徒３名の複数指導

　→１名につき30分の個別指導

　指導時間3分の1、実質料金は割高に。

　　↕

　教師1名・生徒1名の完全個別指導

　⇒完全90分の個別指導（当塾）

　生徒1名に100％の指導時間

親御さんの声

「できる問題が増え勉強に自信がついたようで、期待感があります」

「苦手だった英語と数学が伸び始めたので、正直ホッとしています」

「成績の伸び幅と年間の費用を考えると、転塾して正解でした」

合格実績

八戸高　八戸東高　八戸北高　八戸西高　国立八戸高専　八戸工業高　八戸商業高　八戸工業大学第一高　八戸工業大学第二高　千葉学園高　八戸聖ウルスラ学院・英語科

八戸聖ウルスラ学院中学　八戸工大二高附属中学

指導実績

八戸市立第一中　第二中　第三中　長者中　根城中　白山台中　白銀中　鮫中　大館中　東中　下長中　北稜中　是川中　南浜中　明治中　中沢中　工大二高附属中　階上中　福地中

八戸東高　八戸北高　八戸西高　仙台育英学園高ＩＬＣ

吹上小　中居林小　柏崎小　長者小　根城小　新井田小　旭ヶ丘小　西園小　南郷小

今年度塾生28名（2025年4月現在）

「体験学習」を実施しています

通塾をご検討の方に無料体験学習を実施しております。

当日の学習科目は希望制です。小学生から中高生まで、ご要望にお応えできるよう授業を進めさせていただきます。

ご入塾までの流れ

体験学習（60分）

入塾をご希望の場合、

保護者面談の日程調整

↓

保護者面談（40分程度）

お子様の受講に関わるご説明

保護者の方からのご相談・ご要望

↓

受講開始手続き

体験学習・実施日時はこちら

塾生の声

苦手意識から「自信」へ

（中学３年）

　今まで分からないことが多く、学校の授業についていけないことがあったり、テストで全く解けない問題もありましたが、先生から考え方や解き方を分かりやすく丁寧に教えてもらい、解ける問題が増えてテストの点数が大きく上がりました。この教室に通って、勉強に自信が持てるようになりました。

３年間の積み重ねで受験合格

（小学６年）

　４年生の時から通い始めました。３年間の授業で、先生は分からない問題を理解しやすく、そしてやさしく教えてくれました。本当にこの塾で良かったと思っています。６年生の冬には、志望校の受験に合格することができました。一貫校に進むので、次は大学受験です。中学に上がっても、目標のためにこの塾で学んでいきます。

苦手の克服が高得点に

（高校１年）

　苦手の英語を克服するために通い始めました。長文対策では、先生と一緒に音読練習や和訳などに繰り返し取り組み、テストでは高得点を取れるようになりました。通う前より、勉強の量だけでなく、勉強の質も上げることができました。他教科の苦手にも向き合って、「得意」に変えていけるよう、この教室で学習を続けていきたいです。

受講に関するお問い合わせ

ご相談はお気軽にお尋ねください