文字式中学数学

たむかい学習教室
8月5日
読了時間: 7分

文字式中学数学

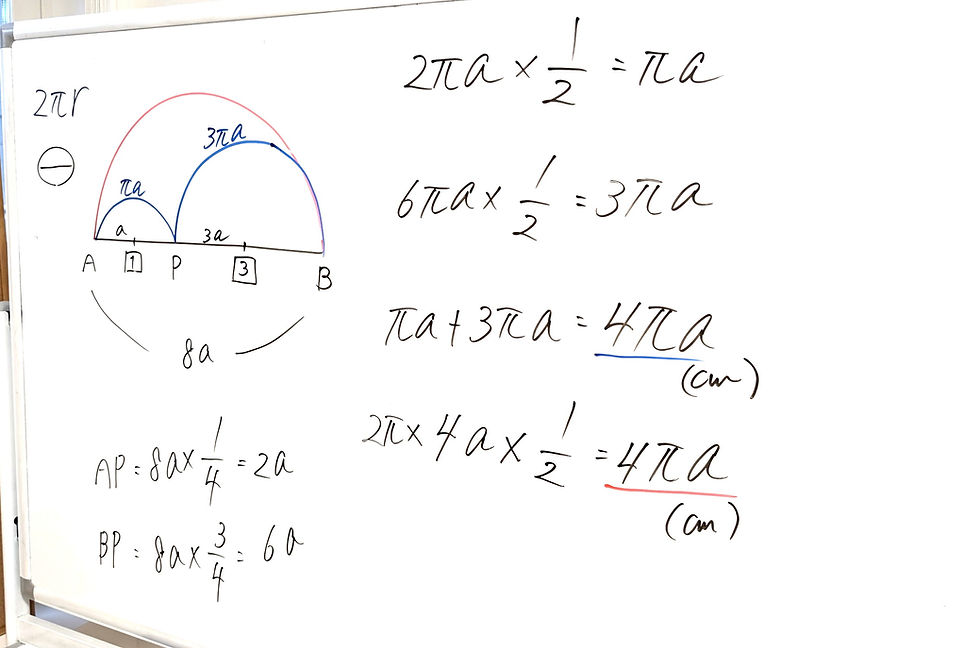
当ブログでは、授業のポイント解説をしています。

学校の夏休みに入り、当塾では「夏期講習」を行っています。文字式には、単項式と多項式があります。単項式は、文字と数字が「２ａ」のようにかけ算でつながる形、多項式は、「ａ²－２ａ＋１」のように単項式どうしが足し算や引き算でつながる形の式のことです。

分配法則

問題

次の計算をしなさい。

1）

３（ｘ＋５ｙ）＋４（ｘ－２ｙ）

2）

５（２ａ－４ｂ）＋６（－３ａ＋５ｂ）

1）

３（ｘ＋５ｙ）＋４（ｘ－２ｙ）

＝３ｘ＋15ｙ＋４ｘ－８ｙ

＝７ｘ＋７ｙ

2）

５（２ａ－４ｂ）＋６（－３ａ＋５ｂ）

＝10ａ－20ｂ－18ａ＋30ｂ

＝－８ａ＋10ｂ

3）

２（３ｘ＋２ｙ）－３（ｘ＋３ｙ）

4）

７（４ｘ－ｙ）－２（９ｘ－７ｙ）

3）

２（３ｘ＋２ｙ）－３（ｘ＋３ｙ）

＝６ｘ＋４ｙ－３ｘ－９ｙ

＝３ｘ－５ｙ

4）

７（４ｘ－ｙ）－２（９ｘ－７ｙ）

＝28ｘ－７ｙ－18ｘ＋14ｙ

＝10ｘ＋７ｙ

5）

（３ｘ－４ｙ）/５＋（ｘ＋ｙ）/２

6）

（ａ＋３ｂ）/８－（２ａ－５ｂ）/４

👇計算手順・解答

文字式の乗除

問題

次の計算をしなさい。

1）４ａ×７ｂ

2）５ａ²×（－２ａ）

3）（－６ｘ）²

4）（－ａ）²×（－７ａ²）

1）

４ａ×７ｂ

＝28ａｂ

2）

５ａ²×（－２ａ）

＝－10ａ³

3）

（－６ｘ）²

＝36ｘ²

4）

（－ａ）²×（－７ａ²）

＝ａ²×（－７ａ²）

＝－７ａ⁴

5）12ａｂ÷４ｂ

6）15ｘ²÷（－３ｘ）

7）45ａ²÷５ａ

8）（－42ｘ²ｙ）÷（－７ｘ）

5）

12ａｂ÷４ｂ

＝３ａ

6）

15ｘ²÷（－３ｘ）

＝－５ｘ

7）

45ａ²÷５ａ

＝９ａ

8）

（－42ｘ²ｙ）÷（－７ｘ）

＝６ｘｙ

問題

次の計算をしなさい。

1）（－ａ²）×（－６ａ）²

2）（－６ｘｙ）÷（－24ｙ）

3）（－15ａｂ²）÷９ａｂ

1）

（－ａ²）×（－６ａ）²

＝－ａ²×36ａ²

＝－36ａ⁴

2）

（－６ｘｙ）÷（－24ｙ）

＝６ｘ×1/24

＝1/4ｘ

3）

（－15ａｂ²）÷９ａｂ

＝－15ｂ×1/9

＝－5/3ｂ

問題

次の計算をしなさい。

1）

６（ａ＋２ｂ－１）－３（２ａ＋３ｂ－２）

2）

1/4（４ｘ－８ｙ）＋1/3（９ｘ＋３ｙ）

3）

３ａ＋ｂ－（２ａ－７ｂ）/３

1）

６（ａ＋２ｂ－１）－３（２ａ＋３ｂ－２）

＝６ａ＋12ｂ－６－６ａ－９ｂ＋６

＝３ｂ

2）

1/4（４ｘ－８ｙ）＋1/3（９ｘ＋３ｙ）

＝ｘ－２ｙ＋３ｘ＋ｙ

＝４ｘ－ｙ

3）

３ａ＋ｂ－（２ａ－７ｂ）/３

👇計算手順・解答

文字式を使った説明

問題

カレンダーで下の図のように３つの数をＬ字形で囲んだとき、囲まれた３つの数の和は、３の倍数になる。このことを、ｎを使って説明しなさい。

〔説明〕

囲まれた３つの数のうち、

もっとも小さい数をｎとすると、

３つの数は、

ｎ、ｎ＋７、ｎ＋８と表せる。

これらの和は、

ｎ＋（ｎ＋７）＋（ｎ＋８）

＝３ｎ＋15

＝３（ｎ＋５）

ｎ＋５は整数だから、

３（ｎ＋５）は３の倍数になる。

したがって、囲まれた３つの数の和は、３の倍数になる。

四角錐を利用した問題

問題

底面の1辺の長さがａcm、高さがｈcmの正四角錐がある。このとき、あとの問いに答えなさい。

1）この正四角錐の体積をＶcm³とするとき、Ｖをａ、ｈを使った式で表しなさい。

2）この正四角錐の底面の1辺の長さを３倍にし、高さを半分にすると、体積はもとの正四角錐の体積の何倍になるか、求めなさい。

1）

四角錐の体積

底面積×高さ×1/3

Ｖ＝ａ²×ｈ×1/3

Ｖ＝1/3ａ²ｈ

2）

底面積の1辺の長さは、３ａ

高さは、1/2ｈ

この立体の体積は、

（３ａ）²×1/2ｈ×1/3

＝3/2ａ²ｈ

よって、

3/2ａ²ｈ÷1/3ａ²ｈ

＝9/2倍

等式の変形

問題

次の等式を〔　〕の中の文字について解きなさい。

1）

５ｘ＋２ｙ＝10　〔ｙ〕

2）

６ａ＋４ｂ－７＝０　〔ａ〕

3）

ａ＝５（ｂ－ｃ）　〔ｂ〕

1）

５ｘ＋２ｙ＝10　〔ｙ〕

２ｙ＝10－５ｘ

　　10－５ｘ

ｙ＝━━━━

　　　２

2）

６ａ＋４ｂ－７＝０　〔ａ〕

６ａ＝－４ｂ＋７

　　－４ｂ＋７

ａ＝━━━━━

　　　　６

3）

ａ＝５（ｂ－ｃ）　〔ｂ〕

ａ＝５ｂ－５ｃ

５ｂ＝ａ＋５ｃ

　　 ａ＋５ｃ

ｂ＝━━━━━

　　　５

円柱を利用した問題

問題

円柱の底面の半径をｒ、高さをｈとすると、体積Ｖは、Ｖ＝πｒ²ｈと表すことができる。あとの問いに答えなさい。

1）Ｖ＝πｒ²ｈをｈについて解きなさい。

2）1）で変形した式を使って、体積が96πcm³、底面の半径が４cmの円柱の高さを求めなさい。

1）

πｒ²ｈ＝Ｖ

　　　Ｖ

ｈ＝━━━

　　 πｒ²

2）

　　 96π

ｈ＝━━━

　　 π×4²

ｈ＝６

よって、

求める高さは、６cm

問題

下の図は、底面の半径がｒcm、高さがｈcmの円柱である。この円柱の底面積（１つの底面の面積）と側面積の比は１：４である。このとき、あとの問いに答えなさい。

1）この円柱の底面積（１つ分）をｒを用いた式で表しなさい。

2）この円柱の側面積を、ｈとｒを用いた式で表しなさい。

3）ｈを、ｒを用いた式で表しなさい。

1）

円の面積の公式より

π×ｒ²

＝πｒ²

πｒ²（cm²）

2）

側面の縦の長さ＝円柱の高さ

側面の横の長さ＝底面の円周

円柱の高さはｈcmだから、

側面の縦の長さはｈcm

底面の円周は、

π×２ｒ

＝２πｒcmだから

側面の横の長さは２πｒcm

よって、求める側面積は、

ｈ×２πｒ

＝２πｒｈ（cm²）

3）

底面1つ分の面積と側面積の比が１：４だから、

１：４＝πｒ²：２πｒｈ

２πｒｈ＝４πｒ²

２ｈ＝４ｒ

ｈ＝２ｒ

円を利用した問題

問題

下の図で、ＰはＡＰ：ＰＢ＝１：３の地点である。Ａ地点からＢ地点までまで行くのに、ＡＢを直径とする半円の弧の㋐と、ＡＰ、ＰＢをそれぞれ直径とする２つの半円の弧を合わせた㋑のコースがある。

ＡＢ＝８ａcmとして、㋐と㋑ではどちらが短いか、または等しいと考えられるか、式を使って説明しなさい。

㋐のコース

ＡＢを直径とする半円の弧の長さは、

π×８ａ×1/2

＝４πａ（cm）

㋑のコース

ＡＰ：ＰＢ＝１：３より、

ＡＰ＝1/4ＡＢ

　　＝1/4×８ａ

　　＝２ａ

ＰＢ＝3/4ＡＢ

　　＝3/4×８ａ

　　＝６ａ

ＡＰを直径とする半円の弧の長さは、

π×２ａ×1/2

＝πａ（cm）

ＰＢを直径とする半円の弧の長さは、

π×６ａ×1/2

＝３πａ（cm）

よって、

㋑のコースの長さは、

πａ＋３πａ

＝４πａ（cm）

したがって、

㋐と㋑のコースの長さは等しい

体験学習受付中！

【たむかい学習教室】

完全1対1 個別指導

教員経験２０年のプロ講師による完全マンツーマン指導！

追加料金なしの安心の授業料で、手厚いサポート！

全科目対応で、幅広い学習ニーズにお応えいたします！

塾生のホンネ

「数学や英語が苦手。何から始めたらいい？」

「長い問題文が苦手。どうしたらいい？」

「学校の授業で難しいことが増えてきた」

「受験が不安。テスト成績を上げていきたい」

完全１対１授業でホンネを解決！

★苦手の克服に最適★

★受験に強い個別指導★

★経験豊富な講師の一貫指導★

★安心の授業料で全力サポート★

★苦手の克服に最適★

　５教科対応、完全マンツーマンで指導いたします。弱点を着実に克服でき、「わかる・できる」につながります。学校の授業が定着しやくすなり、成績アップも期待できます。

★受験に強い個別指導★

　入試の出題範囲は広く、十分な対策時間と学習量が必要になります。受験に向けて、対策時間と学習量をしっかりと確保できるのは、完全１対１授業の強みです。

★経験豊富な講師の一貫指導★

　教員経験20年の講師が確かなノウハウで、難解な内容もわかりやすく丁寧に指導いたします。初めての受講生からも「分かりやすい」「納得の解説」と好評です。

★安心の授業料で全力サポート★

　入塾費や高額な教材費、授業料以外にいただく追加料金は一切ございません。安心の授業料で全力サポートいたします。

　＜１か月授業料（税込）＞

　90分授業：14,800円（月4回）

120分授業：17,600円（月4回）

　(例)１回・90分授業の場合

　教師１名・生徒３名の複数指導

　→１名につき30分の個別指導

　指導時間3分の1、実質料金は割高に。

　　↕

　教師1名・生徒1名の完全個別指導

　⇒完全90分の個別指導（当塾）

　生徒1名に100％の指導時間

親御さんの声

「できる問題が増え勉強に自信がついたようで、期待感があります」

「苦手だった英語と数学が伸び始めたので、正直ホッとしています」

「成績の伸び幅と年間の費用を考えると、転塾して正解でした」

合格実績

八戸高　八戸東高　八戸北高　八戸西高　国立八戸高専　八戸工業高　八戸商業高　八戸工業大学第一高　八戸工業大学第二高　千葉学園高　八戸聖ウルスラ学院・英語科

八戸聖ウルスラ学院中学　八戸工大二高附属中学

指導実績

八戸市立第一中　第二中　第三中　長者中　根城中　白山台中　白銀中　鮫中　大館中　東中　下長中　北稜中　是川中　南浜中　明治中　中沢中　工大二高附属中　階上中　福地中

八戸東高　八戸北高　八戸西高　仙台育英学園高ＩＬＣ

吹上小　中居林小　柏崎小　長者小　根城小　新井田小　旭ヶ丘小　西園小　南郷小

今年度塾生28名（2025年4月現在）

「体験学習」を実施しています

通塾をご検討の方に無料体験学習を実施しております。

当日の学習科目は希望制です。小学生から中高生まで、ご要望にお応えできるよう授業を進めさせていただきます。

ご入塾までの流れ

体験学習（60分）

入塾をご希望の場合、

保護者面談の日程調整

↓

保護者面談（40分程度）

お子様の受講に関わるご説明

保護者の方からのご相談・ご要望

↓

受講開始手続き

体験学習・実施日時はこちら

塾生の声

苦手意識から「自信」へ

（中学３年）

　今まで分からないことが多く、学校の授業についていけないことがあったり、テストで全く解けない問題もありましたが、先生から考え方や解き方を分かりやすく丁寧に教えてもらい、解ける問題が増えてテストの点数が大きく上がりました。この教室に通って、勉強に自信が持てるようになりました。

３年間の積み重ねで受験合格

（小学６年）

　４年生の時から通い始めました。３年間の授業で、先生は分からない問題を理解しやすく、そしてやさしく教えてくれました。本当にこの塾で良かったと思っています。６年生の冬には、志望校の受験に合格することができました。一貫校に進むので、次は大学受験です。中学に上がっても、目標のためにこの塾で学んでいきます。

苦手の克服が高得点に

（高校１年）

　苦手の英語を克服するために通い始めました。長文対策では、先生と一緒に音読練習や和訳などに繰り返し取り組み、テストでは高得点を取れるようになりました。通う前より、勉強の量だけでなく、勉強の質も上げることができました。他教科の苦手にも向き合って、「得意」に変えていけるよう、この教室で学習を続けていきたいです。

受講に関するお問い合わせ

ご相談はお気軽にお尋ねください